Anonymity in the open with Tornado Cash

Cryptocurrency transactions can be tracked from point to point because all transaction data is public. The transaction data needs to be public to ensure the financial integrity of the system, which is non-negotiable. So, given that we cannot get rid of transparency, how do we achieve privacy?

In Bitcoin, one way to achieve privacy is through Coinjoins. Many users come together, add their own coins as inputs to a specific large transaction, get equivalent coins as outputs on the other side of the same large transaction, and confirm this transaction on the blockchain. If enough users participate in such coinjoins frequently, every user gets a measure of privacy about where their coins came from, or where their coins went. The problem is – if these users don’t know each other, they need a central coordinator to build this large transaction. To make the central coordinator as trustless as possible, coinjoin protocols use blind signatures.

Blind Signatures

Blind signatures are an ingenious idea by David Chaum. It works the following way: Alice puts her digital artifact (say a message that says “Bob is a fool”) inside a digital envelope so that the message is not visible. The digital envelope could be the equivalent of encrypting the message. She takes this message-in-the-envelope to Bob and asks him to sign the envelope, which he does.

Alice goes back home with the signed envelope and morphs into Carol. She then performs some magic cryptography that moves Bob signature from outside the envelope to the message inside the envelope. As Carol, she goes back to Bob and shows him a signed copy of the message “Bob is a fool”. Bob can verify that it’s his own signature on the message, and only he could have signed it. But he doesn’t know when he signed it, or what it looked like when he had signed it earlier. The only thing Bob knows is that he has signed it sometime in the past.

This bit of cryptographic magic is as impressive as it would be in real life. A paper-and-pen signature moves from the envelope to the paper inside the envelope at the wave of a magic wand. Voila!

Chaumian Coinjoins

In a Chaumian coinjoin, the user comes to the coordinator with a plain text input coin and a “enveloped” output coin. If the the financial value of the input coin is the same as the output coin, the coordinator signs the user’s output coin’s envelope. The coordinator also includes the input coins in the large coinjoin transaction that it is building. The user then comes back to the coordinator with a changed network identity and the output coin in plain text, without the envelope. The coordinator recognizes its own signature, and adds the output coin to the large coinjoin transaction.

Note that the coordinator has no idea about which input coins correspond to which output coins. Once the transaction has enough such blindly matched inputs and outputs, the transaction is “closed”, and then passed around to the input parties for their signatures. After the signatures are collected, the transaction is broadcast to the network and confirmed. Blind signatures prevent a user from submitting 1 BTC as input and receiving 2 BTC as output.

Can Chaumian coinjoins be done in the open?

Let’s say we wanted the coordinator’s software to be fully open source, or be decentralized like Bitcoin, or run as a smart contract on a platform like Ethereum, can we do that?

We can’t.

The private key used for blind signatures should not be known to users. Else the whole scheme collapses. There is no way to store the coordinator’s private key in the open and make Chaumian coinjoins work.

Enter ZK-SNARKs

ZK-SNARK stands for Zero Knowledge Succinct Non-interactive Argument of Knowledge. The idea is that you have a pair of programs (say ZKP and ZKV), written in a normal programming language like C++, Rust, or Python. Alice runs ZKP with some private inputs known only to her, and maybe some public inputs known to everyone (like time of the day, or the latest Bitcoin blockhash). After running with these inputs, the ZKP produces an output (say OP) and also a proof (say P) that Alice ran ZKP with only those inputs that can generate the output OP. The proof P has no information about the actual secret inputs that Alice gave ZKP. Both output OP, and the proof P are just bytes – and in the case of ZK-SNARKs, P is quite small as well.

The program ZKV takes P and OP as inputs and generates either “True” or “False” as its output. If Alice did indeed run ZKP with only those inputs that generated the output OP, ZKV will print “True”. Otherwise, ZKV will print “False”.

How ZKP/ZKV are created, and how does this actually work – is left as a future series of articles. The question for today is, how is this ZK-SNARKs apparatus useful in the context of coinjoins?

Tornado Cash

In Tornado Cash, two ZKVs (ZKV1 and ZKV2) are deployed on the blockchain as a single smart contract. The code is open, anyone can read it, and has no secret information embedded in it. Alice deposits some money in this smart contract, along with a special hash that she creates. This hash is created by hashing the concatenation of two random strings R and N. That is, H = sha256^[1]Pedersen hashes are used in most ZK Proofs. Their algebraic nature makes them more amenable to ZK proofs as compared to the more information theoretic nature of the SHA family of hashes.(R||N). Why concatenate two strings and then hash them? We will see that later.

One example would be R = “0123456”, and N = “11-12-13-14-15”. If you concatenate R and N, you get the string “012345611-12-13-14-15”. If you hash it with SHA256, you get the hash: c6305d7b22616c176520a64f7689f755bdc5dc3ffac9a86236ea6ed804ff8be6.

Alice deposits 1 ETH to the Tornado Cash smart contract with this additional hash input c6305d7b22616c176520a64f7689f755bdc5dc3ffac9a86236ea6ed804ff8be6. Tornado Cash stores this string in a Merkle Tree, and returns the Merkle Path to Alice. Merkle Trees, invented by Ralph Merkle in the 1970’s are a way to encode a set using a compact representation. If you have a set of a million numbers, you can encode them in a Merkle Tree and represent this entire set as a single hash string. Numbers are hashed pairwise, and these hashes are hashed again pairwise, all the way up to a single hash at the top of tree.

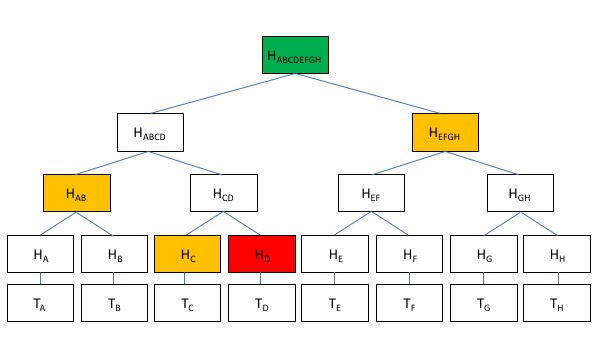
In the above example, 8 strings Ta, Tb, Tc, Td, Te, Tf, Tg, and Th are stored in the Merkle Tree, with the entire set being represented by the hash Habcdefgh. It was calculated using pairwise hashing from the leaves of the tree all the way to the root. To prove that this tree contains Td, the prover gives the hashes Hd, Hc, Hab, and Hefgh to the verifier. These 4 hashes and the publicly known hash of the root Habcdefgh, are enough to prove to the verifier that Hd is present in the Merkle tree. Otherwise, it would be impossible to construct these series of hashes so that:

Habcdefgh = sha256(sha256(Hab, sha256(Hc, sha256(Td))), Hefgh)

If you can construct this proof, it means that Td in in the Merkle tree. Set membership is proven through the knowledge of the Merkle “path” from the element to the publicly known root. Proof of Knowledge, in other words.

Alice had deposited 1 ETH to Tornado Cash along with H = sha256(R||N) as additional input. She also had the Merkle proof of the membership of H in the Merkle tree stored in the smart contract. This Merkle tree is public, and anyone can view it. To get her money back under a new identity, Alice morphs herself to Carol (new connection, different IP address, different browser, etc.) and runs ZKP1 with the Merkle proof as private input along with the R and N as private inputs. ZKP1 outputs a proof P1 that the Merkle proof with sha256(R||N) as the leaf checks out. Carol (previously known as Alice) also runs ZKP2 to prove that sha256(N) = X, where N is the private input, and X is public data. ZKP2 outputs a proof P2 that proves that sha256(N) = X.

Alice gathers the following pieces of data: P1, P2, and X. She hands P1 to ZKV1 and {P2, X} to ZKV2 on the blockchain. The ZKVs can verify that P1 and P2 could only have been generated if both the following two statements are true.

• ZKV1 verifies that Carol knows the Merkle proof of some element in the Merkle tree. This element is the hash of two strings: some R and some N.
• ZXV2 verifies that Carol also knows N such that sha256(N) = X.

The smart contract checks if anyone had used X in the past to withdraw money, and if no one had done so, allows Carol to withdraw 1 ETH from the smart contract. The contract then adds X to its “spent list”, which is a permanent list that will live for the entire lifespan of the smart contract.

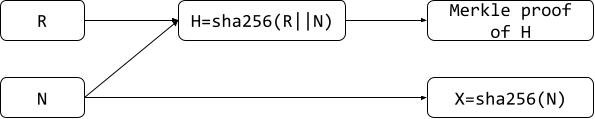
The point of the prover/verifier pair {ZKP2, ZKV2} is to prevent Carol from depositing once and withdrawing twice. The point of the other prover verifier pair {ZKP1, ZKV1} is to prove it to the smart contract that Alice knows two strings R and N such that sha256(R||N) is somewhere in the Merkle tree, and she can prove that with the Merkle proof – but she actually reveals none of these actual inputs. She reveals just the proofs that she knows these inputs. Anyone who observes the withdraw transaction sees two ZK proofs and one string X – and none of these were used in the deposit transaction, thereby breaking the link between the deposit and withdraw transactions.

Say someone tried to exhaustively check all the elements in the public Merkle tree to see which one matches against Carol’s withdraw transaction. They would fail because the elements in the Merkle tree are of the form sha256(R||N), and there is no way to connect any of them with X = sha256(N) from Carol’s transaction.

ZCash

In Tornado Cash, the smart contract is public and sits on the blockchain. In ZCash the same idea of using R and N, with N preventing double spending is used to construct a privacy preserving cryptocurrency from the ground up. In this case, the ZKP’s are in the users’ wallet software, and the ZKV’s are on the blockchain’s primary node software – which enforces consensus rules when run by many nodes. Even in this case, the primary node software’s code is public, and hence cannot contain a private key to perform Chaumian style blind-signature based privacy operations.

How is the magic done?

The magic is in the cryptographic primitives. For now, we assume their functioning as given and just use their API’s to build protocols. In future articles, we will look under the hood of some of these primitives, especially ZK-SNARKs. Using these primitives, we get to be truly anonymous. Anonymity due to code that is entirely in the open, with no secrets kept anywhere. I am almost shocked that this is even possible.